Înmulțirea. Cum se face înmulțirea?
Înmulțirea este operația aritmetică care constă în mărirea unui număr (deînmulțit) de atâtea ori cât alt număr (înmulțitor), pentru a obține un rezultat numit produs. Înmulțirea mai poate fi definită ca o adunare succesivă. Înmulțirea este reprezentată prin semnele: „x”, „•”.
Cum se face înmulțirea?
Fiind date două numere naturale, de exemplu 4 și 3, vom înțelege prin produsul numerelor 4 și 3 , care se numesc factorii produsului, numărul natural notat cu 4 x 3 sau 4 • 3, care se obține astfel:
4 • 3 = 4 + 4 + 4. (4 este deînmulțit iar 3 este înmulțitor.)
Spunem că 4 • 3 se obține prin înmulțirea numerelor 4 și 3. Dacă facem produsul numerelor naturale 3 și 4 vom obține
3 • 4 = 3 + 3 + 3 + 3.
Deci:
Produsul unui număr natural cu un număr natural, diferit de 0 și 1, se exprimă printr-o sumă în care primul număr natural apare ca termen de atâtea ori de câte ori arată al doilea număr natural.
Apoi
4 • 0 = 0 și 4 • 1 = 4.
Deci:
Produsul unui număr natural cu zero este zero. Produsul unui număr natural cu unu este numărul natural considerat.
Calculând sumele prin care exprimăm pe 4 • 3 și 3 • 4, obținem:
4 + 4 + 4 = (4 + 4) + 4, (4 + 4) + 4 = 8 + 4, 8 + 4 = 12.
Aceste egalități pot fi scrise sub forma:
4 + 4 + 4 = (4 + 4) + 4 = 8 + 4 = 12.
Analog:
3 + 3 + 3 + 3 = (3 + 3) + 3 + 3 = 6 + 3 + 3 = (6 + 3) + 3 = 9 + 3 = 12.
Deci
4 • 3 = 3 • 4
O astfel de proprietate este adevărată oricare ar fi perechea de numere naturale considerate și se enunță în general:
Oricare ar fi numerele naturale a și b avem
a • b = b • a.
Această proprietate a înmulțirii numerelor naturale se numește comutativitatea înmulțirii numerelor naturale.
Fiind date trei numere naturale 4, 2, 2 avem:
(4 • 2) • 2 = (4 • 4) • 2 = 8 • 2 = 8 + 8 = 16.
4 • (2 • 2) = 4 • (2 + 2) = 4 • 4 = 4 + 4 + 4 + 4 = (4 + 4) + 4 + 4 = 8 + 4 + 4 = (8 + 4) + 4 = 12 + 4 = 16.
Deducem că
(4 • 2) • 2 = 4 • (2 • 2).
O astfel de proprietate este adevărată și pentru alte trei numere naturale, oricare ar fi ele, și se enunță în general:
Oricare ar fi numerele naturale a, b și c avem
(a • b) • c = a • (b • c).
Această proprietate a înmulțirii numerelor naturale se numește asociativitatea înmulțirii numerelor naturale. Din cauză că
(a • b) • c = a • (b • c),
vom conveni ca prin a • b • c să înțelegem sau (a • b) • c, sau a • (b • c). Deci, în loc de (4 • 2) • 2 vom scrie 4 • 2 • 2 și în loc de 4 • (2 • 2) vom scrie tot 4 • 2 • 2.
Numărul natural 1 este element neutru la înmulțirea numerelor naturale, deoarece, oricare ar fi numărul natural a, avem:
a • 1 = 1 • a = a.
Înmulțirea unui număr natural cu un număr natural de o cifră
Să înmulțim numărul natural 216 cu 3. Pentru obținerea produsului acestor numere naturale se procedează astfel: înmulțim, mai întâi, cu 3 ultima cifră din 216, adică înmulțim pe 6 cu 3. Obținem 18. Scriem la rezultat pe 8 și înmulțim cu 3 următoarea cifră din 216, adică pe 1 cu 3, obținând 3. La 3 adunăm pe 1 din 18, obținând 4, și scriem la rezultat pe 4 în fața lui 8. Înmulțim, apoi, pe 2 cu 3, obținând 6, și scriem la rezultat pe 6 înaintea lui 4. Produsul numerelor 216 și 3 este 648.
Se spune că, numărul 648 este de 3 ori mai mare decât 216. De asemenea, numărul 648 este de 216 ori mai mare decât 3.
Înmulțirea a două numere naturale
Să înmulțim numerele naturale 216 și 341.
Calculele se așază în felul următor:
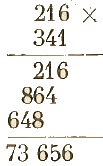
Fiecare cifră din numarul natural 341, adica 3, 4 și 1 se va înmulți cu fiecare cifră din numărul natural 216, adică 2, 1, 6. Înmulțirea se face de la dreapta la stânga după cum urmează:: cifra unu de la finalul numărului 341 se va înmulți cu fiecare cifra din numărul natural 216. Mai exact: 1 se va înmulții cu 6, rezultând 6, apoi 1 se va înmulți cu 1, rezultând 1, iar în cele din urmă 1 se va înmulți cu 2, rezultând 2. Va rezulta produsul 216.
Sub produsul rezultat 216 în urma înmulțirii cu 1, vom trece produsul rezultat în urma înmulțirii cu 4. Așadar, continuăm înmulțirea cu urmatoarea cifră de la dreapta la stânga din numărul natural 341, adică cu 4. 4 se va înmulți cu 6 rezultând 24, vom scrie 4 și vom ține în minte numărul 2 pe care îl vom adăuga la rezultat înmulțirii dintre 4 și 1 (1 fiind următoarea cifra de la dreapta la stânga din 216) care este egal cu 4 la care adaugâm numărul 2 din minte și rezultă 6, vom scrie 6. Mergem mai departe înmulțind 4 cu 2, rezultând 8 pe care îl vom scrie. Produsul înmulțirii cu cifra 4 este 864. În acest fel se va continua și cu ultima cifra din numărul natural 341, adică cu cifra 3 care se va înmulți cu fiecare număr în parte din numărul natural 216, rezultând produsul 648 care se va scrie sub produsul înmulțirii cu 4.
Distributivitatea înmulțirii față de adunare și scădere
Pentru numerele 4, 2, 1 avem
4 • (2 + 1) = 4 • 3 = 4 + 4 + 4 = (4 + 4) + 4 = 8 + 4 = 12.
4 • 2 + 4 • 1 = 8 + 4 = 12.
Deducem că
4 • (2 + 1) = 4 • 2 + 4 • 1.
O astfel de proprietate este adevărată și pentru alte trei numere naturale, oricare ar fi ele, și se enunță în general:
Oricare ar fi numerele naturale a, b și c avem
a • (b + c) = a • b + a • c.
Această proprietate se numește distributivitatea înmulțirii față de adunare.
Problemă rezolvată
Cineva cumpără o dată 2 m de stofă, iar altă dată 3 m din aceeași stofă. Știind că metrul de stofă costă 200 lei, să se afle cât a costat stofa.
Rezolvare
Putem judeca în două moduri:
a) Aflăm, mai întâi, câți metri de stofă au fost cumpărați și înmulțim rezultatul cu cât costă 1 m de stofă. Obținem:
200 • (2 + 3) = 1000 (lei)
b) Aflăm cât a costat de fiecare dată stofa și adunăm rezultatele.
Obținem:
200 • 2 + 200 • 3 = 1000 (lei)
Se vede că:
Am pus în evidență, aici, distributivitatea înmulțirii față de adunare.
Avem:
4 • (2 – 1) = 4 • 1 = 4, 4 • 2 – 4 • 1 = 8 – 4 = 4.
Deducem că
4 • ( 2 – 1) = 4 • 2 – 4 • 1.
În general:
Oricare ar fi numerele naturale a, b, c și b ≥ c avem
a • (b – c) = a • b – a • c.
Această proprietate se numește distributivitatea înmulțirii față de scădere.
Sursa: Editura Didactică și Pedagocică, București 1989 Clasa a-V-a, Prof. univ. dr. C.P. Popovici, Prof. I.C. Ligor, Prof. I.G. Borca – Scăderea